What is the time-weighted rate of return (TWR)?
The time-weighted return (TWR) measures the compound growth rate of a portfolio. Growth rates can be distorted by cash inflows and outflows. This distortion is eliminated by calculating the TWR. To do this, the returns are divided into intervals, always at the times when money has flowed in or out. This adjusted return is therefore better suited to comparing the returns of different securities portfolios.
The calculation of the time-weighted return (TWR)

A new period is created for each interval in which cash inflows or outflows have taken place. The return is calculated separately for each of these periods. The returns for each individual period are then multiplied together.
Example of calculating the time-weighted rate of return (TWR) compared to the simple rate of return
Beispiel 1
An investor invests CHF 10,000 in a securities portfolio every year for three years. Assume that the securities portfolio grows by 10% in the first year. At the end of the year, the portfolio has a value of CHF 11,000. An additional CHF 10,000 is newly invested. At the beginning of the second year, the portfolio would therefore have a value of CHF 21,000. In the second year, the value of the portfolio falls by 5% to CHF 19,950. In the third year, the last investment of CHF 10,000 is made and the portfolio makes a profit of 15%. After the 3 years, the portfolio has a value of around CHF 34,443. The profit is around CHF 4,443. The simple return is 14.8% (4,443/30,000). However, the time-weighted return is 20.2%.
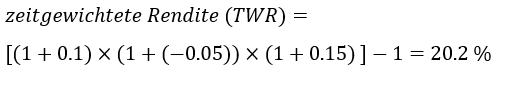
Beispiel 2
An investor invests CHF 30,000 for three years in the same securities portfolio from example 1. As in example 1, the value of the portfolio increases by 10% in the first year (value of the portfolio: CHF 33,000), decreases by 5% in the second year (value of the portfolio: CHF 31,350), and increases again by 15% in the third year (value of the portfolio: CHF 36,053). As no money was added or withdrawn in this example, the time-weighted return is the same as the simple return. The profit amounts to CHF 6,053 and the return for both the time-weighted and the simple return is 20.2% (6,053/30,000).
Comparison of example 1 and example 2
If the simple returns from examples 1 and 2 are now compared, the securities portfolio from example 2 appears to be more lucrative. However, this is not the case. The examples show the same portfolio. The investor who invested the full amount at the beginning (example 2) earned more money. However, this is not always the case. Under certain circumstances, investing according to a kind of savings plan, as in example 1, can be more lucrative. Suppose, for example, that the value of the securities portfolio fell by 5% in the first year, then rose by 10% in the second year, and rose by 15% in the third year. The portfolio of the investor in example 1 would then have been worth CHF 36,168 after the 3 years. An asset manager is responsible for putting together securities portfolios, but has only limited influence on how much money is invested and when. Consequently, the simple return cannot be used directly to compare securities portfolios. It is therefore advisable to look at the time-weighted return when assessing theperformance of assetmanagers.
The example shows that it can be difficult to determine how much money can be earned with a securities portfolio if several deposits or withdrawals of funds are made over time. This is where the calculation of the TWR is advantageous. However, the TWR should not be confused with the investor’s actual return.

