What is discounting?
Discounting is a term used in financial mathematics. Discounting is the process of determining the present value of a payment or cash flow to be received in the future. In other words, discounting is used to calculate thepresent value of the future payment (present value). Given the time value of money, a franc is worth more today than it would be worth tomorrow, as it can be invested alternatively. From a business perspective, an asset only has value if it can produce payments in the future. The value of these future payments in today’s terms is calculated by applying a discount factor to future payments. In general, a higher discount means that there is a greater risk associated with an investment and its future payment.
The formula for discounting
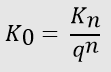

Example 1: Present value of a one-off payment
Assume an investor invests CHF 100,000 in a property. The investor is guaranteed the sale of the property after 3 years at a value of CHF 120,000. The calculation interest rate is 5%. To decide whether this investment is worthwhile, the investor should calculate how much the future payment of CHF 120,000 is worth today.
Calculation of discount factor:
Discount factor: 1 / (1 + 0.05)³= 0.863837599
The discount factor is multiplied by the payout in 3 years:
CHF 120’000 * 0.863837599 = CHF 103’661
As the present value of the future payment (CHF 103,661) is higher than the amount invested (CHF 100,000), the investment is worthwhile. If the investor invests the money securely at 5% for 3 years, the investor receives a value of (CHF 100,000 * (1+0.05)³) CHF 115,763. This amount is less than the CHF 120,000 offered.
Example 2: Present value of several payments
Assume an investor makes a one-off investment of CHF 100,000 in a construction project. In return, the investor receives an annual payment surplus of CHF 40,000 for 3 years . The calculation interest rate is 5%.
The discount factor must be recalculated for each year:
Discount factor year 1: 1 / (1 + 0.05) = 0.952380952
Discount factor year 2: 1 / (1 + 0.05)² = 0.907029478
Discount factor year 3: 1 / (1 + 0.05)³ = 0.863837599
If the discount factor is now multiplied by the payout for the year, this gives the present value per year:
CHF 40’000 * 0.952380952 = CHF 38’095
CHF 40’000 * 0.907029478 = CHF 36’281
CHF 40’000 * 0.863837599 = CHF 34’554
The first disbursement is worth CHF 38,095 today. The disbursement in the second year is worth CHF 36,281 today, while the disbursement in the third year is worth CHF 34,553 today. This adds up to a total of CHF 108,930, which is higher than the CHF 100,000 originally invested, making the investment in this project worthwhile.

