Definition of compound interest
Compound interest is the interest paid on a deposit or loan, which is calculated based on both the initial capital and the interest accrued in previous periods. In other words, compound interest is the interest paid out on the interest already received in previous periods.
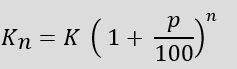
The compound interest formula for annual interest
Kn: Capital after interest payment (final capital)
K: Capital before interest payment (initial capital)
p: Interest
n: Number of years
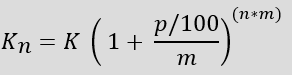
The compound interest formula for interest during the year
Kn: Capital after interest payment (final capital)
K: Capital before interest payment (initial capital)
p: Interest
n: Number of years
m: Number of interest periods per year
Example:
Assuming you invest CHF 100 (initial capital) at 10 % interest, you will receive CHF 10 (interest) at the end of the year and end up with an amount of CHF 110 (final capital). If you leave the money invested, you will receive 10% interest again at the end of the second period. However, the interest is not calculated on the basis of the initial capital (CHF 100), but on the basis of the final capital (CHF 110). You will therefore be paid interest of CHF 11. Compound interest therefore increases a little more each year, which is also known as the compound interest effect. This effect is clearly illustrated in the two figures below. For this reason, it is worth starting to invest at a young age.
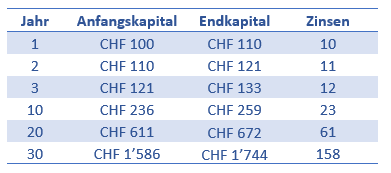
Table Example compound interest from www.valueinvestments.ch
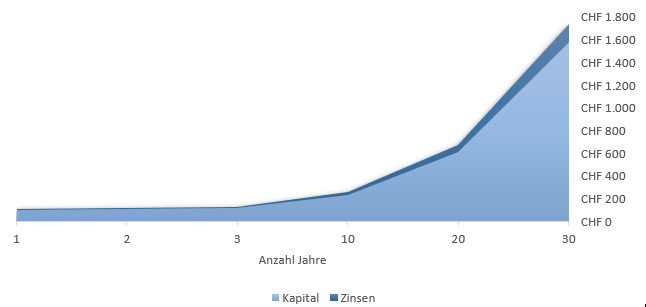
Graphic example of compound interest from www.valueinvestments.ch
The level of the interest rate is also decisive. The following table compares the amount of the final capital for an initial investment of CHF 100 over 50 years at 5 % interest, 10 % interest and 20 % interest. In year 50, the final capital for an investment of CHF 100 at an interest rate of 20 % is approx. 77 times higher compared to an interest rate of 10 %.
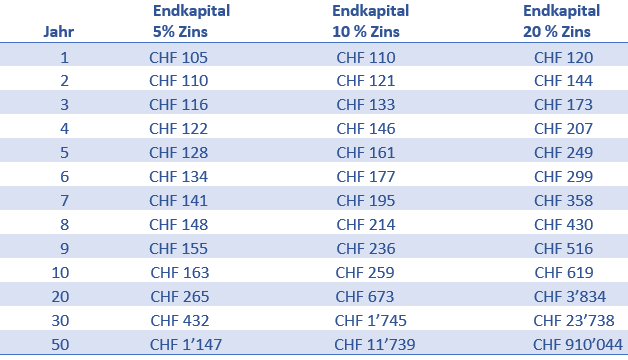
Table Example of compound interest on initial capital vs. final capital from www.valueinvestments.ch
The following chart compares the amount of the final capital with an initial investment of CHF 100 over 5-10 years at an interest rate of 5 %, 10 % and 20 %. Non-linear growth is evident.
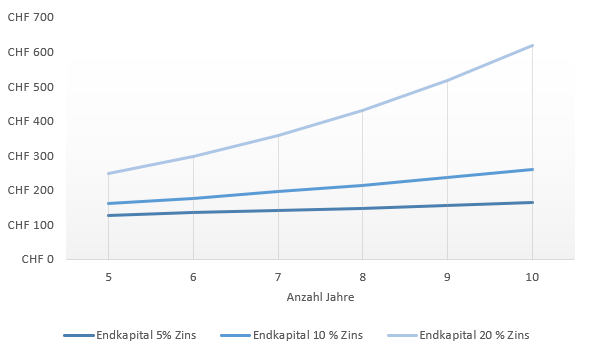
Graphic example of compound interest Initial capital vs. final capital from www.valueinvestments.ch
Accumulation periods
The number of periods increases the compound interest effect. Consequently, compound interest increases with the number of compounding periods. The following figure shows the final capital with interest over 10 years at an annual interest rate of 10% for three different compounding periods.
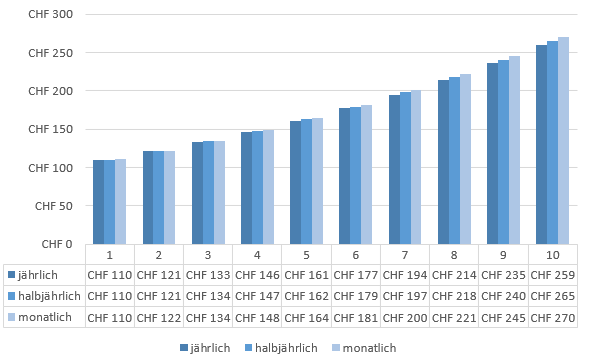
Chart of compounding periods from www.valueinvestments.ch

