What is the Capital Asset Pricing Model?
The Capital Asset Pricing Model (CAPM) is a model of the capital market and can be used to calculate the cost of capital. It is therefore used to explain expected returns on securities. The expected return is a linear function of the risk premium of the marketportfolio. The market portfolio represents all the risks of the securities on the market. An important factor in the CAPM is beta, which indicates how strongly a particular security reacts to or correlates with market fluctuations. If a security reacts strongly to market fluctuations, the security is more risky and therefore the expected return also increases.
More specifically, the CAPM describes the relationship between systematic risk and the expected return on assets, particularly equities. The CAPM is widely used throughout the financial world to value securities and to determine the expected return on assets, taking into account the risk of these assets and the cost of capital.
Portfolio theory: systematic risk and unsystematic risk
Systematic risk is the aggregation of all risks that affect all individual securities in an asset class together. It therefore excludes the risk that only affects one individual asset. As the systematic risk affects the entire asset class, it cannot be reduced, for example, by diversification – the distribution of money – within the asset class. The only way to reduce this risk is to diversify across different asset classes.
The unsystematic risk is the part of the risk that can be avoided by diversifying the securities portfolio.
The Capital Asset Pricing Model (CAPM) is based on the assumption that the risks of individual securities can be reduced through a diversified securities portfolio – i.e. through a good mix of securities.
The formula of the Capital Asset Pricing Model (CAPM)
When an investor invests money, a risk premium is demanded for the systematic risks. In other words, investors want to be rewarded for the risks they take.

In the CAPM, the risk premium is calculated by calculating the difference between the expected return on the market portfolio and the risk-free interest rate. The risk-free interest rate represents the return that an investor can expect if the money is invested risk-free – also known as the time value of money. The difference is therefore the excess return that can be expected if the money is invested in a market portfolio instead. In doing so, the investor takes risks. However, as not every investment reacts to market fluctuations in the same way, a parameter is needed to factor in these fluctuations: This parameter is called beta. Assuming that the market can be represented by a market portfolio, the expected return of the overall market is converted to the expected return of individual investments. Beta indicates how strongly an individual investment fluctuates when the market as a whole goes up or down.
The formula of the Capital Asset Pricing Model (CAPM) is therefore as follows:

The beta of an investment is a measure of how much risk the investment adds to a portfolio in relation to the market risk. For example, if a share is riskier than the market, it has a beta greater than one. This means that if the market rises or falls by 1 %, the share moves by more than 1 %. If a share has a beta of less than one, the formula assumes that it reduces the risk of a portfolio. The share rises or falls less than the market as a whole.
The aim of the CAPM formula is to assess whether a share is fairly valued if its risk and the time value of money are in line with its expected return. return are compared.
Example of the CAPM calculation
Suppose an investor wants to buy ashare worth 300 francs. Furthermore, the share is riskier than the market: this means that the beta of the investment is greater than 1. In this example, the beta is 1.2. The risk-free interest rate is 2%. The investor believes that the market will rise by 5% annually.
Based on these assumptions, the investor can calculate the expected return using the CAPM formula. In this example, the expected return is 5.6%.
Expected return = 2 + 1.2 x (5-2)
Expected return = 5.6%
The CAPM and the efficient frontier
The CAPM can also be used to construct a portfolio and can help with risk management. Suppose an investor is able to use the CAPM to perfectly optimize the return of a portfolio in relation to the risk. If the investor were able to do this, the portfolio would lie on a curve known as the efficient frontier. The following graph shows, among other things, this efficient frontier:
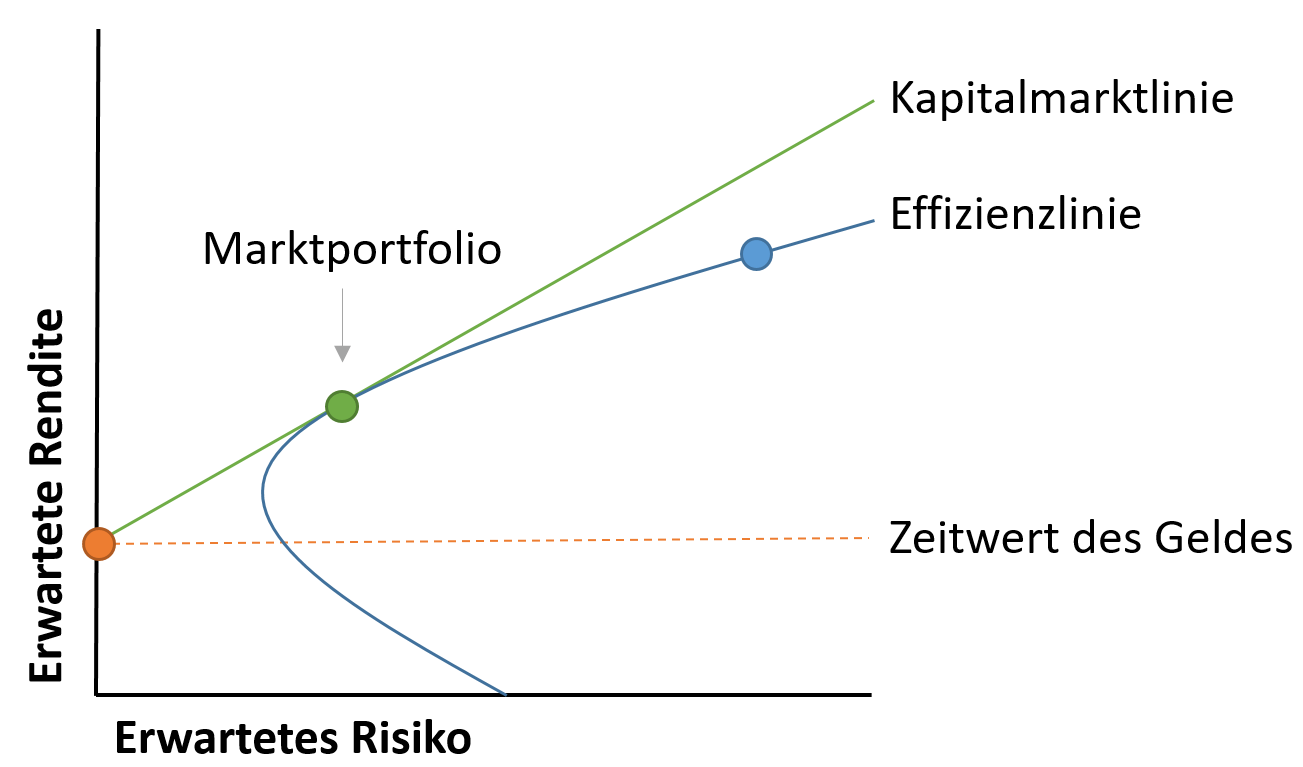
The chart shows that higher expected returns require a higher expected risk. Modern portfolio theory (MPT) assumes that the expected return of a securities portfolio increases with increasing risk. The starting point is the risk-free interest rate on the y-axis with the expected return – also known as the time value of money. Any securitiesportfolio that lies on the capital market line is therefore better than any possible securities portfolio to the right of this line. This is the case because if there is a parallel deviation to the right, the expected return remains the same but the risk increases. The optimal securities portfolio is referred to as the market portfolio.
The capital market line and the efficiency line are difficult to determine in practice, but these lines illustrate the trade-off between increased return and increased risk. Since in reality it is not possible to create a portfolio that fits the capital market line perfectly, investors often take on too much risk with the aim of achieving additional returns. Suppose the green dot in the figure shows portfolio 1, and the blue dot in the figure represents portfolio 2. Suppose portfolio 1 has an expected return of 5%, with a standard deviation (risk) of 7%. Portfolio 2 has an expected return of 7%, but with a risk of 10%. In this example, the risk has increased more than the return: an investor is therefore not sufficiently compensated for the additional risk in portfolio 2.
Like the CAPM, the efficient frontier can only be calculated theoretically, as it is based on the same assumptions. If a portfolio is on the efficient frontier, it would offer the maximum return for its level of risk. However, it is impossible to know whether a portfolio is on the efficient frontier or not, as future returns cannot be predicted.
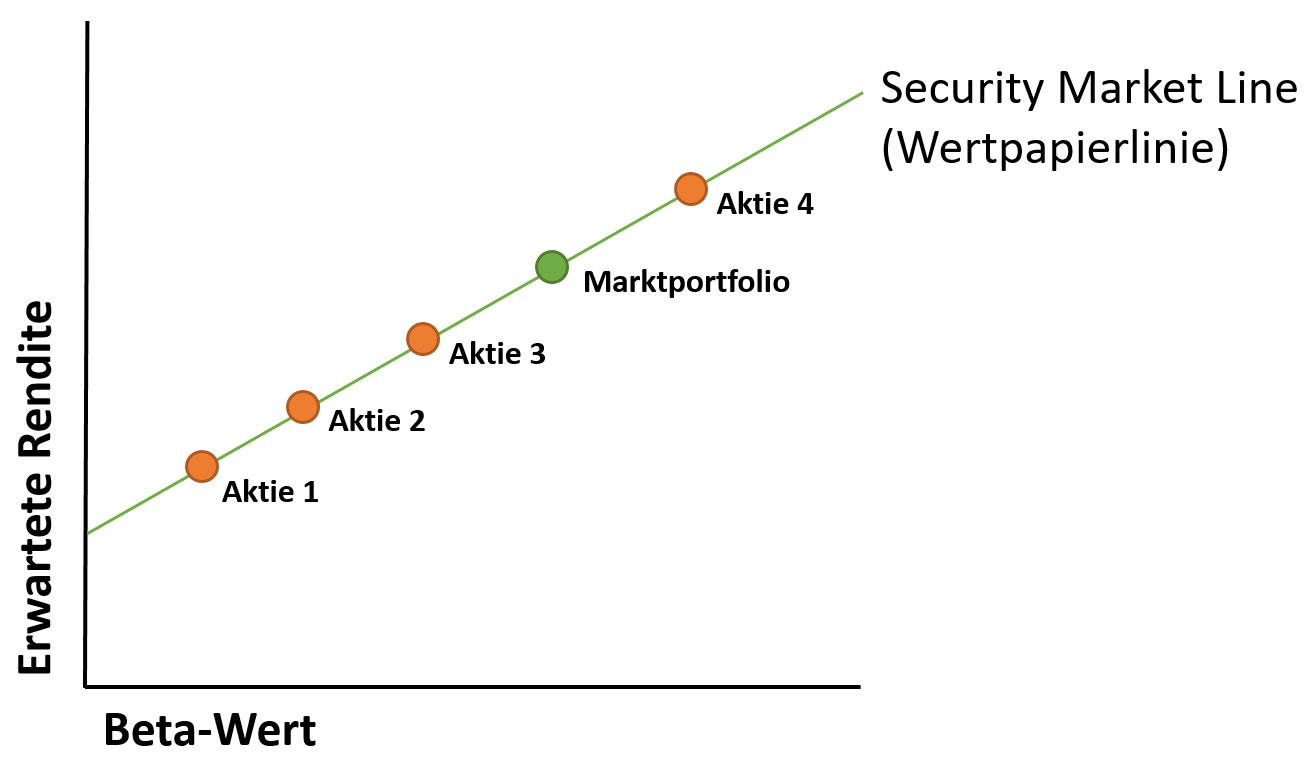
The efficiency line diagram can also be displayed differently to illustrate the trade-off for individual assets. In this case, the beta value is shown on the x-axis. The capital market line is now referred to as the security line – better known as the security market line (SML). As the beta increases, so does the expected return. A higher beta means more risk. A portfolio of high beta stocks may be somewhere on the capital market line where the trade-off is acceptable – even if it does not represent the theoretical ideal. Unfortunately, beta also requires assumptions to be made. Since these assumptions do not necessarily apply, the model loses its value.
Putting together an ideal portfolio that corresponds to your individual risk capacity and risk appetite is not easy. It is advisable to consult an expert such as an independent asset manager.
Disadvantages of the CAPM formula
As with most models, the CAPM formula is based on several assumptions that are not always realistic. In general, two assumptions are made in modern financial market theory:
- The assumption that securities markets are competitive and efficient . This means that relevant information about the companies is quickly disseminated and absorbed and is therefore already included in the price.
- The assumption that markets are dominated by rational, risk-averse investors who seek to maximize the satisfaction of returns on their investments.
The inclusion of beta in the formula assumes that the risk can be measured using the price volatility of a share. However, price movements in both directions are not equally risky. The period in the past used to determine the volatility of a share is not standardized, as share returns and risk are not normally distributed.
The CAPM also assumes that the risk-free interest rateremains constantover thediscountingperiod. However, this is not always the case. An increase in the risk-free interest rate, for example, increases the cost of the capital employed in the investment and could make the investment appear overvalued.
The market portfolio used to determine the market risk premium is only a theoretical valueand not an asset that can be bought or invested in as an alternative to the stock. In most cases, investors use a large stock index to replace the market, which is not a correct comparison.
In addition, the CAPM assumes that future cash flows can be estimated for the discounting process, which is not the case and which would also make the CAPM superfluous. There is therefore no measurability of expected returns. The expected value is only derived from the sample of past data. The “true” expected values are unknown. It is therefore important to understand that the expected return is only an estimate.

